Un triángulo es un polígono que tiene tres lados y tres ángulos. 


CLASIFICACIÓN

De acuerdo a la longitud de sus lados y al tipo de ángulos que tiene los podemos clasificar en:  

TRIÁNGULOS SEMEJANTES

Son aquellos que tienen los mismos ángulos aunque la longitud de sus lados varía.

Por ejemplo:

TRIÁNGULOS CONGRUENTES

Dos triángulos son congruentes (iguales) si y sólo si, existe una correspondencia entre sus vértices de manera tal que cada par de lados y ángulos correspondientes sean iguales. 

El símbolo de congruencia es

 
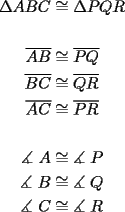
Triángulos oblicuángulos

En la resolución de triángulos oblicuángulos se pueden distinguir 4 casos:

Caso1: Cuando se conocen 2 ángulos y un lado.


Caso 2: Cuando se conocen 2 lados y un ángulo opuesto a uno de ellos.



Caso 3: Cuando se conocen 2 lados y el ángulo formado por ellos.



Caso 4: Cuando se conocen los 3 lados.



Ley de senos

Para el Caso 1 y 2 se usa la ley de Senos en la resolución de éstos triángulos:

SenA = SenB = SenC
   a            b           c

Te recomendamos ver:
Animaciones ley de senos


Ley cosenos

Para el caso 3 y 4 se usa la ley de Cosenos en la resolución de éstos triángulos:

a²=b²+c²-(2bc·CosA)
b²=a²+c²-(2ac·CosB)
c²=a²+b²-(2ab·CosC)

Te recomendamos ver:
Animación ley cosenos 1
Animación ley cosenos 2



 

Ejemplos:

Supongamos que en el triángulo de la figura 1 . Encontrar la longitud del tercer lado.

Solución:

Para calcular el valor del tercer lado, podemos emplear la ley de cosenos:

EJERCICIOS

Encuentra los valores de los triángulos dados los siguientes valores en caso de ser factibles los valores dados en caso contrario comente porqué no es correcto los datos dados o porqué no es útil la ley  de senos.